Alfavita Newsroom Τα άρθρα που έχουν γραφεί για το θέμα αυτό είναι εκατοντάδες, τα περισσότερα από τα οποία ξεκινούν με μια σύντομη βιογραφία του Ερατοσθένη και στη συνέχεια, εξαίροντας την ευφυΐα του και το μεγαλείο του πολιτισμού που τον εξέθρεψε, καταλήγουν σε μια πρόχειρα δοσμένη και συχνά ωραιοποιημένη παρουσίαση της μέτρησης.
Δεν είναι έτσι φυσικά όλα τα άρθρα αντίστοιχα: για παράδειγμα εδώ[1] ή εδώ[2] μπορεί να βρει κάποιος δύο πολύ καλές αναλύσεις που δίνουν μερικές σχετικά άγνωστες πτυχές της μέτρησης του Κυρηναίου μαθηματικού. Σε αυτό το άρθρο δεν θα δώσουμε παρά μερικά ψήγματα για παραπέρα αναζήτηση, γιατί στη πραγματικότητα αυτό που επιθυμούμε είναι να κάνουμε μια ωδή στα μαθηματικά.
Και το άρθρο αυτό, λοιπόν, δεν ξεκινάει με κάποια βιογραφία, αλλά ούτε και με κάποιο κήρυγμα υπέρ της μαγείας των μαθηματικών.
Ξεκινάει με μια ιστορία
Η Ιστορία
Έτος 1987, σε κάποιο λύκειο της Αθήνας, σε κάποιο τμήμα της α΄ λυκείου. Ο καθηγητής της τάξης ονομάζεται Νίκος Καλογερόπουλος, ένα νέο τότε παιδί 28 ετών, εκπληκτικός άνθρωπος και πολύ καλός εκπαιδευτικός, παρουσίαζε στον πίνακα μια πληροφορία από το σχολικό βιβλίο φυσικής που αφορούσε «τη πρώτη μέτρηση της ακτίνας της γης από τον Έλληνα γεωμέτρη Ερατοσθένη». Το βιβλίο έγραφε και ο καθηγητής μετέδιδε πάνω κάτω τα εξής:
Ο Ερατοσθένης γνώριζε ότι η Γη είναι σφαιρική. Γνώριζε επίσης πως την ημέρα του καλοκαιρινού ηλιοστάσιου στη πόλη Συήνη της Αιγύπτου, οι ακτίνες του ήλιου έπεφταν κατακόρυφα στο έδαφος – ο ήλιος καθρεφτιζόταν ολόκληρος σε ένα πηγάδι χωρίς να αφήσει πουθενά σκιές στα τοιχώματά του. Την ίδια μέρα του χρόνου, στην Αλεξάνδρεια, ο Ερατοσθένης αφού έμπηξε ένα ραβδί κάθετα στο έδαφος, παρατήρησε ότι το ραβδί αυτό κάνει σκιά. Μετρώντας το μήκος της σκιάς και γνωρίζοντας το μήκος του ραβδιού που είχε τοποθετήσει κατακόρυφα στο έδαφος, μπόρεσε να μετρήσει την ακτίνα και την περιφέρεια της γης.
Και αφού τελείωσε τη διήγηση και τα αντίστοιχα σχήματα στον πίνακα ο καθηγητής, κάθισε σκεπτικός στο κέντρο της αίθουσας κοιτώντας το σχήμα που είχε μόλις φτιάξει και συμπλήρωσε με τη φράση «αλλά δεν ξέρω πως το υπολόγισε!»
Αξίζει εδώ μια παρένθεση. Ένα από τα μεγαλεία που μπορείς να δεις σε έναν καθηγητή, και το είδαμε τότε για πρώτη μας φορά, είναι η παραδοχή της άγνοιας: έχοντας συνηθίσει ως τότε τον καθηγητή ξερόλα που «γνωρίζει» τα πάντα χωρίς να είναι ικανός να καλύπτει τις απορίες μας, η πρωτόγνωρη για εκείνη την εποχή φράση που ξεστόμισε μας άφησε τις καλύτερες εντυπώσεις.
Κλείνει η παρένθεση και συνεχίζεται η ιστορία.
Θυμάμαι ότι ήμουν σε κάποια γωνιά της αίθουσας παρακολουθώντας μαγεμένος την παρουσίαση της μεθόδου που είχε ακολουθήσει ο Ερατοσθένης και κοίταζα γεμάτος περιέργεια τα σχήματα που είχαν δημιουργηθεί. Και μόλις ο καθηγητής ξεστόμισε τη φράση «αλλά δεν ξέρω πως το υπολόγισε», πετάγομαι σχεδόν αμέσως και ανακοινώνω «ξέρω εγώ!» Και χωρίς να περιμένω τη προτροπή που αμέσως ήρθε, σηκώθηκα στον πίνακα και εξήγησα τον τρόπο που έγινε ο υπολογισμός.
Το σπόιλερ της ιστορίας είναι ότι στο τέλος του άρθρου, θα εξηγήσω ότι κατά πάσα πιθανότητα η λύση που παρουσίασα ήταν, αν δεν θέλουμε να μιλήσουμε με επιείκεια, εντελώς ανόητη. Παρ΄ όλα αυτά, μπορούμε, χρησιμοποιώντας τα δεδομένα που έχει αφήσει η παράδοση, να δούμε συνοπτικά ένα τρόπο υπολογισμού της ακτίνας της γης.
Λίγη Γεωμετρία
Κάθε μαθητής που έχει διδαχτεί γεωμετρία β΄ λυκείου γνωρίζει πως το μήκος L του τόξου ενός κύκλου ακτίνας R που αντιστοιχεί σε τόξο μ μοιρών (ή στο οποίο βαίνει επίκεντρη γωνία μο) δίνεται από τη σχέση
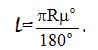
Η παράδοση αφηγείται πως η γωνία που μέτρησε ο Ερατοσθένης από το τρίγωνο που σχημάτισε το ραβδί, η σκιά του και η ακτίνα του ήλιου ήταν 7,2ο, ίδια με την επίκεντρη γωνία που σχημάτισαν οι ακτίνες της σφαιρικής γης που καταλήγουν στην Αλεξάνδρεια και στη Συήνη (τη πόλη με το πηγάδι, εκεί που οι ακτίνες του ήλιου πέφτουν κατακόρυφα). Τη δε απόσταση Συήνης – Αλεξάνδριας τη μέτρησε σε 800 χιλιόμετρα («5040 στάδια»), αντικαθιστώντας λοιπόν στον παραπάνω τύπο και λύνοντας ως προς την ακτίνα βρίσκουμε
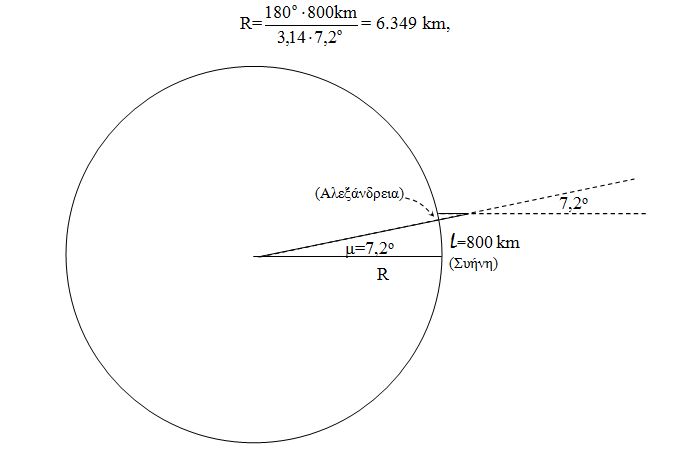
με πολλούς μελετητές της παραπάνω μέτρησης να ισχυριστούν ότι η τιμή αυτή είναι αξιοθαύμαστα κοντά στη πραγματική τιμή της ακτίνας της γης, που σήμερα μετριέται στα 6.378 χιλιόμετρα.
Μαγικό.
Το Επίτευγμα
Το μόνο εκπληκτικό και αξιοθαύμαστο, και σε καμία περίπτωση μαγικό, της παραπάνω προσπάθειας, είναι ότι έχουμε για πρώτη κατά τα φαινόμενα φορά μια επιστημονική προσέγγιση της εκτίμησης της ακτίνας της γης, και κατ΄ επέκταση της περιφέρειάς της. Ο Ερατοσθένης (ή οι προγενέστεροί του) δεν πίστεψε ότι η γη δεν είναι επίπεδη, αλλά το συμπέρανε παρατηρώντας τις διαφορετικές γωνίες που σχηματίζουν τις ίδιες χρονικές στιγμές σε διαφορετικούς τόπους οι ακτίνες της γης με το έδαφος. Και οι προγενέστεροί του δεν συμπέραναν αυθαίρετα ότι η γη είναι σφαιρική: το συμπέραναν παρατηρώντας ότι οι ηλιακές ακτίνες σε μια συγκεκριμένη ζώνη της γης πέφτουν υπό την ίδια ακριβώς γωνία δύο φορές το χρόνο, ενώ στις υπόλοιπες περιοχές της η γωνία που σχηματίζει ο ήλιος με το έδαφος είναι διαφορετική για κάθε μέρα του χρόνου, όπως μόνο σε μια σφαιρική επιφάνεια μπορεί να συμβεί όπως είχαν ήδη αποδείξει. Και ο δε υπολογισμός της ακτίνας, έγινε με δεδομένα που βασίστηκαν από τη μια μεν στις ακριβέστερες για τα μέτρα της εποχής δυνατές μετρήσεις, αλλά από την άλλη σε επιστημονικές μεθόδους οι οποίες σε καμία χρονική στιγμή της ιστορίας, σε κανένα μέρος του σύμπαντος και από κανένα νοήμον ον, δεν θα μπορέσουν ποτέ να τεθούν σε αμφισβήτηση. Και υπό αυτή την έννοια,
ακόμη κι ένας σημερινός 16άχρονος που κουβαλάει μια παράδοση 2.500 χιλιάδων μόλις χρόνων ανθρώπινης ιστορίας, μπορεί να κάνει μια ανακάλυψη για την οποία δεν θα τον αμφισβητήσει ποτέ κανείς. Και η δύναμη που θα μπορεί να του δίνει αυτή η γνώση, θα είναι απλά διαχρονική, καθολική και απόλυτη.
Παρ΄ όλα αυτά.
Η ομορφιά βρίσκεται μόνο στην αλήθεια, και η όποια προσπάθεια διαστρέβλωσή της περισσότερο αφαιρεί την ίδια την ομορφιά παρά προσθέτει οτιδήποτε, πέρα από την ικανοποίηση πρωτόγονων ενστίκτων. Παρά το ότι η Γεωμετρία που χρησιμοποιήθηκε για τη παραπάνω μέτρηση είναι πέρα για πέρα ακριβής, η ίδια η μέτρηση βρίθει λαθών. Αξίζει να δούμε μερικά.
Η Απομυθοποίηση
Η αντικατάσταση και μόνο του ανύπαρκτου για την εποχή του Ερατοσθένη «3,14» που χρησιμοποιήθηκε στον παραπάνω υπολογισμό με τη πιθανή τιμή 22/7 που πιθανόν να χρησιμοποιούσε ο Ερατοσθένης ως προσέγγιση του π, δίνει ήδη μια απόκλιση μερικών χιλιομέτρων από τη παραπάνω τιμή. Εξ΄ άλλου, το να ισχυριστεί κανείς ότι «η ακτίνα της γης είναι 6.378 χιλιόμετρα» είναι από μόνο του μια ανοησία: η γη όπως γνωρίζουμε σήμερα δεν είναι σφαιρική αλλά ελλειπτική, σε κάθε διαφορετικό λοιπόν γεωγραφικό μήκος αντιστοιχεί και διαφορετική ακτίνα, ενώ η παραπάνω τιμή αντιστοιχεί στη μέση τιμή της ακτίνας της γης, τιμή διαφορετική με αυτή που αντιστοιχεί στο γεωγραφικό πλάτος που βρίσκεται η Αλεξάδρεια και που έκανε τη μέτρηση ο Ερατοσθένης.
Αλλά ακόμη κι αν το σχήμα της γης δεν ήταν έλειψη, δεν θα ήταν επίσης και κύκλος: η γη είναι σφαίρα, και αυτή η απλή παρατήρηση απαιτεί αντίστοιχη προσοχή στο τι εννοούμε όταν λέμε ότι μετράμε «απόσταση»: για τους γνωρίζοντες, μια ευθεία πάνω στη γη δεν είναι παρά ένας μέγιστος κύκλος, και πρακτικά για να μπορέσει να γίνει ο παραπάνω υπολογισμός θα πρέπει οι δύο πόλεις να βρίσκονται στο ίδιο γεωγραφικό μήκος. Αυτό ήταν κάτι που το γνώριζε ο Ερατοσθένης όταν έκανε τους υπολογισμούς του, έκανε όμως λάθος στην εκτίμηση ότι οι δύο πόλεις βρίσκονται πράγματι στο ίδιο γεωγραφικό μήκος.
Επίσης: τα «5040 στάδια» στα οποία υπολογίστηκε η απόσταση Συήνης – Αλεξάνδρειας, δεν είναι παρά ένα ωραίο αστείο: κατ΄ αρχάς ο τρόπος που υπολογίστηκε η απόσταση, όπως είναι γνωστό, έγινε μετρώντας τη μέση ταχύτητα με την οποία κινείται ένα καραβάνι από καμήλες και το χρόνο που χρειάζεται για να διανύσει την απόσταση μεταξύ των δύο πόλεων. Όλοι θα δεχτούν ότι η μέθοδος αυτή δεν μπορεί να χαρακτηριστεί σε καμία λογική περίπτωση ως αξιόπιστη, αλλά για να μεγαλώσει η ομορφιά θα προσθέσουμε ότι κανείς μα κανείς δεν γνωρίζει σε τι στάδια μετρήθηκε η απόσταση αυτή: σε Αττικά στάδια, στάδια της Περγάμου, Αιγυπτιακά, μήπως Περσικά; Σε όλους αρέσει παρ΄ όλα αυτά να θεωρούμε ότι η μέτρηση έγινε με τα στάδια που δίνουν τη καλύτερη προσέγγιση για την ακτίνα, τα οποία μεταφράζονται τελικά σε 800 χιλιόμετρα, με τη πραγματική απόσταση μεταξύ των δύο πόλεων να είναι 729 χιλιόμετρα.
Κι επειδή μερικά λάθη στον αριθμητή ενός κλάσματος μπορούν να απαλειφθούν με αντίστοιχα λάθη στον παρανομαστή, η γωνία που σχηματίζουν οι ηλιακές γωνίες με το έδαφος κατά την θερινή ισημερία στην Αλεξάδρεια, έχει πια μετρηθεί ίση με 7,5ο και όχι με τις 7,2ο που ελήφθησαν υπ΄ όψιν για τη παραπάνω μέτρηση. Έτσι, χωρίς βλάβη της γενικότητας και χωρίς να μειώσουμε την αξία της προσπάθειας, μπορούμε χωρίς καμία αμφιβολία να ισχυριστούμε πως το γεγονός ότι το τελικό αποτέλεσμα της μέτρησης προσεγγίζει τόσο καλά το πραγματικό, οφείλεται σε πολύ μεγάλο ποσοστό σε καλή τύχη.
Ένας Πανέμορφα Λάναθασμένος Υπολογισμός
Η ιστορία με το καθηγητή να περιγράφει τα δεδομένα κι εμένα να βρίσκω τη «λύση» αναδύθηκε από τα υπόγεια της λήθης του μυαλού μου κάποια «επετειακή» 21 Ιουλίου, όπου και διάβασα ένα αντίστοιχο άρθρο για τη μέτρηση της γης του Ερατοσθένη, και ταυτόχρονα με την ανάδυσή της μου γεννήθηκε ένα απλό ερώτημα: η παραπάνω λύση που περιγράφηκε (και είναι η απλούστερη που μπορεί να γνωρίζει ένας μαθητής λυκείου) απαιτεί γνώσεις γεωμετρίας β΄ λυκείου, που εγώ δεν τις είχα γιατί όπως θυμάστε οι προσεκτικότεροι από εσάς πήγαινα ακόμη α΄ λυκείου. Θα μπορούσε να πει κανείς βέβαια πως στη παραπάνω γνώση θα μπορούσε άνετα να καταλήξει κι ένας μαθητής β΄ γυμνασίου με μια απλή μέθοδο των τριών (οι 360ο αντιστοιχούν σε μήκος L=2πR, οι μο σε πόσο; ), αλλά αν βρισκόταν κάποιος τέτοιος θα του απαντούσα άνετα πως, αν είχα κάνει μια τέτοια σκέψη, θα τη θυμόμουν γεμάτος περηφάνια την επόμενη χρονιά όταν θα διδασκόμασταν τον τύπο που είχα «ανακαλύψει» ένα χρόνο νωρίτερα, έτσι θα μπορούσα να συμπεράνω ότι δεν χρησιμοποίησα τη παραπάνω μέθοδο. Η μόνη μέθοδος που μπορώ σήμερα να σκεφτώ ότι είχα χρησιμοποιήσει τότε, αφορούσε τα όμοια τρίγωνα.
Και μπορώ να με φανταστώ να σηκώνομαι στο πίνακα, να πάρω κιμωλία, να αρχίζω με πάθος να σχεδιάζω και παράλληλα να αγορεύω: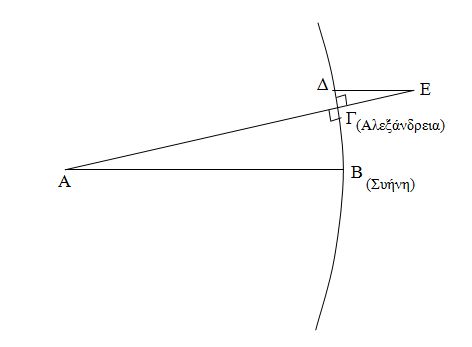
Επειδή η περιφέρεια της γης είναι μεγάλη και συγκριτικά η απόσταση των δύο πόλεων είναι μικρή, μπορούμε να υποθέσουμε ότι στο σχήμα το ΒΓ είναι ένα ευθύγραμμο τμήμα, το δε ΑΒΓ ένα τρίγωνο ορθογώνιο με ορθή γωνία το Γ.
Τα τρίγωνα ΑΒΓ κ΄ ΓΔΕ είναι όμοια, γιατί έχουν τις Γ1, Γ2 ορθές και τις Α, Ε ίσες ως εντός, εκτός κ΄ επί τα αυτά. Από την ομοιότητα των σχημάτων προκύπτει ότι…
Αν δεν μας ενοχλεί να γίνουμε αυστηροί απέναντι σε έναν 15άχρονο, μπορούμε να πούμε ξεκάθαρα ότι λέει ανοησίες. Ακόμη κι αν δεχτούμε τον ισχυρισμό πως προσεγγιστικά το τμήμα ΒΓ είναι ευθύγραμμο, δεν θα περάσει από καμία σοβαρή κρίση η υπόθεση ότι το ΑΒΓ είναι ορθογώνιο με ορθή το Γ: η γωνία Γ είναι κάθετη ακριβώς όσο είναι και η Β, το δε «τρίγωνο» ΑΒΓ δεν είναι καν τρίγωνο αφού έχει δύο γωνίες ορθές, οι όποιες ιδιότητες λοιπόν ισχύουν μεταξύ ομοίων τριγώνων ή έχουν καταρρεύσει, ή θα μπορούν εξίσου να εφαρμοστούν ακόμη κι αν θεωρήσουμε ως ορθή γωνία το Β, δίνοντας τραγικά διαφορετικά αποτελέσματα.
Αν όμως θέλουμε να είμαστε ευγενικοί και τον αφήσουμε να συνεχίσει τον καταφανώς λανθασμένο ισχυρισμό του, θα μας πει ότι
…ισχύει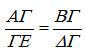 
, απ΄ όπου παίρνουμε ότι η ακτίνα της γης ΑΓ ισούται με
.
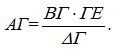Αφού ο Ερατοσθένης γνώριζε το τμήμα ΒΓ, που είναι η απόσταση μεταξύ Αλεξάνδρειας και Συήνης, το μόνο που είχε να κάνει ήταν να υπολογίσει το μήκος του μπαστουνιού του και το μήκος της σκιάς που άφηνε, να τα αντικαταστήσει στον τύπο και να βρει την ακτίνα της γης.
Και το μόνο που έχουμε να κάνουμε εμείς, για να κλείσουμε το άρθρο, είναι να πάρουμε τα δεδομένα που έχουμε. Η γωνία Ε είχε μετρηθεί από τον Ερατοσθένη ίση με 7,2ο, αν υποθέσουμε ότι το «μπαστούνι του» είχε μήκος 1 μέτρο, από τον τύπο
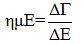
βρίσκουμε ότι η σκιά θα ήταν ίση με 0,12533 μέτρα, ή 0, 00012533 χιλιόμετρα. Αντικαθιστούμε λοιπόν στον παραπάνω τύπο και βρίσκουμε
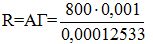
το οποίο μας δίνει ότι η ακτίνα ισούται με R=6.383 χιλιόμετρα.
Μπίνγκο!!!
Κώστας Θεολόγος,
Μαθηματικός
Όλες οι σημαντικές και έκτακτες ειδήσεις σήμερα
Παν.Πατρών: Μοριοδοτούμενο σεμινάριο ΕΙΔΙΚΗ ΑΓΩΓΗΣ με μόνο 65Є εγγραφή - έως 22 Απριλίου
Μοριοδοτούμενο σεμινάριο Ειδικής Αγωγής (ΕΛΜΕΠΑ) με μόνο 50Є εγγραφή- αιτήσεις ως 22/4
2ος Πανελλήνιος Γραπτός Διαγωνισμός ΑΣΕΠ: Τα 2 μαθήματα εξέτασης και η ύλη
Proficiency και Lower μόνο 95 ευρώ σε 2 μόνο ημέρες στα χέρια σας (ΧΩΡΙΣ προφορικά, ΧΩΡΙΣ έκθεση!)
ΕΥΚΟΛΕΣ ΠΙΣΤΟΠΟΙΗΣΕΙΣ ΙΣΠΑΝΙΚΩΝ και ΙΤΑΛΙΚΩΝ για εκπαιδευτικούς - Πάρτε τις άμεσα
